æĶ¹©ō¦¤Ų¤ĪĢO”Ź7”Ė”سĪĪØÅŖbĶż¤ĪÅŠ¾ģ·Š°Ž
³ĪĪØÅŖbĶż¤Īɽø½µĖ”
”ÖæĶ¹©ō¦¤Ī¼Āø½¤Ė¤Ļ”Ų³ĪÄźÅŖ¤ŹbĶż”Ł¤ņ”Ų³ĪĪØÅŖ¤ŹbĶż”Ł¤Ė³ČÄ„¤¹¤ėĶפ¬¤¢¤ė”פȔ¢½é¤į¤Ę»Ų¼~¤·¤æ¤Ī¤Ļ”¢1986ćQ¤ĖbŹø”ŹProbabilistic Logic”Ė¤ņČÆɽ¤·¤æ„Ė„ė„¹”¦„Ķ„ė„½„󞔏Nils J. Nilsson”¢Åö»ž„¹„æ„ó„Õ„©”¼„ɽj³Ų¤Ī„³„ó„Ō„唼„愵„¤„؄󄹤Ī¶µčb”Ė¤Ą¤Ć¤æ¤Č¤¤¤ļ¤ģ¤Ę¤¤¤ė”£”Ź»²¹Ķ«@ĪĮ1”Ė”£
1986ćQ¤Č¤¤¤¦¤Č”¢100ĖüĮĒ»Ņ¤ņ®¤Ø¤ė„Į„Ƅפ¬ĪĢ¾¤µ¤ģ»Ļ¤į¤æ»žĀå¤Ē¤¢¤ė”£ ½j·æ„³„ó„Ō„唼„æ¤Ī„Ą„¤„󄵄¤„ø„ó„°¤¬»Ļ¤Ž¤ź”¢ĶĶ”¹¤Ź½øĄŃvĻ©Ąß¼Ć¤ĪEDA„Ä”¼„ė¤Ī„½„Õ„Č„¦„Ø„¢¤¬³×æ·¤µ¤ģ”¢ICOT”Źæ·Ą¤Ā儳„ó„Ō„唼„æ¶\½Ń³«ČƵ”¹½”Ė¤Ė¤č¤ė„Ø„„¹„Ń”¼„Č„·„¹„Ę„ą³«ČƤ¬ææ¤ĆŗĒĆꤥ¤Ć¤æ»žĀå¤Ē¤ā¤¢¤Ć¤æ”£
”Ö³ĪĪØÅŖ¤ŹbĶż¤¬ĶהפȤĪ„Ė„ė„¹”¦„Ķ„ė„½„óž¤Ī¼ēÄ„¤¬”¢¤½¤Ī„Ē„£„ø„æ„ė³×Ģæ¤ĪóÕ«“ü¤Ė¤Ę¤É¤Ī¤č¤¦¤Ė°·¤ļ¤ģ¤æ¤Ī¤«É®Ēv¤ĻÄ“¤ŁĄŚ¤ģ¤Ę¤¤¤Ź¤¤”£ ¤·¤«¤·¤Ź¤¬¤é”¢”ÖōÅŖ¤Ź„Ž„·„ó¤ĪĄß¼¤Ė¤Ļ”¢³ĪĪØÅŖ¤ŹbĶż¤¬Ć¤¤¤é¤ģ¤ė¤Ļ¤ŗ¤Ą”פȤĪø«²ņ¤Ļ”¢½øĄŃvĻ©³«ČƤ¬»Ļ¤Ž¤ėi¤ĪĆŹ³¬¤Ē¤Ļ”¢¤ą¤·¤ķ”¢ÉįÄĢ¤Ą¤Ć¤æ¤Ī¤Ē¤Ļ¤Ź¤¤¤Ą¤ķ¤¦¤«”©””
Īć¤Ø¤Š”¢Īņ»ĖÖ½é¤į¤ĘÅÅ»ŅvĻ©¤ņƤ¤¤æ„³„ó„Ō„唼„æ¤Ī³«ČƤņ¹Ō¤Ć¤æ„Õ„©„󔦄Ī„¤„Ž„óž¤Ļ”¢1952ćQ¤Ė„«„ź„Õ„©„ė„Ė„¢¹©²Ź½j³Ų¤Ē¹Ō¤Ć¤æ¹Ö±é”Ź"Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components"”¢»²¹Ķ«@ĪĮ2”Ė¤ņæŹ¤į¤ė¤Ė¤¢¤æ¤Ć¤Ę”¢“šĖÜvĻ©¤ņ³ĪĪØÅŖbĶż„ā„Ē„ė”ŹæŽ1”Ė¤Č¤·¤Ę¤¤¤æ”£ ¤½¤Ī“šĖÜbĶżvĻ©„ā„Ē„ė¤Ļ”¢1943ćQ¤Ī„Ž„«„ķ„Ć„Æ&„Ō„Ć„Ä”ŹMacCulloch&Pitts”Ė¤ĪæĶ¹©„Ė„唼„ķ„ó„ā„Ē„ė¤Ē¤¢¤Ć¤æ”Ź»²¹Ķ«@ĪĮ3”¢4”Ė”£
Č¾Ę³½øĄŃvĻ©¤¬ø«¤¤¤Ą¤µ¤ģ¤ėi¤ĪĆŹ³¬¤Ē¤Ļ”¢¤Ź¤¼æĶ¹©ō¦¤ņ¹½Ą®¤¹¤ė¤Ė¤Ļ³ĪĪØÅŖbĶż¤ņɽø½¤¹¤ė±éQ»Ņ¤¬ĶפČø«¤Ę¤¤¤æ¤Ī¤Ą¤ķ¤¦¤«”©
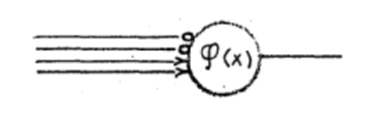
æŽ1””„Õ„©„󔦄Ī„¤„Ž„󞤬1952ćQ¤Ī¹Ö±é¤Ē椷¤æ„Ŗ”¼„Č„Ž„æ (Automata) ¤ņ¹ēĄ®¤¹¤ė¤æ¤į¤Īš¤Ī“šĖÜ„ā„Ē„ė””¤³¤Ī„ā„Ē„ė¤ņ”¢“šĖÜß_“± (Basic organ) ”¢¤ā¤·¤Æ¤Ļ”¢Ć±½ŠĪ„Ŗ”¼„Č„Ž„Č„ó (Automaton) ¤Čā}¤ó¤Ē¤¤¤æ”Ź»²¹Ķ«@ĪĮ2”Ė”£ ¤³¤Ī„ā„Ē„ė¤Ļ”¢1943ćQ¤ĖÄó椵¤ģ¤æ¤Č¤µ¤ģ¤Ę¤¤¤ė„Ž„«„ķ„Ć„Æ&„Ō„Ć„Ä”ŹMacCulloch&Pitts”Ė¤ĪæĶ¹©„Ė„唼„ķ„󔏤ā¤·¤Æ¤Ļ”¢·Į¼°„Ė„唼„ķ„ó”Ė¤Ī„ā„Ē„ė¤Č“šĖÜÅŖ¤Ė¤Ļʱ¤ø¤Ē¤¢¤ė”Ź»²¹Ķ«@ĪĮ3¤Č4”Ė”£
½ŠÖZ”§Automata Studies, Princeton University Press”Ź»²¹Ķ«@ĪĮ2”Ė
„Ž„«„ķ„Ć„Æ&„Ō„ƄĤĪæĶ¹©„Ė„唼„ķ„ó„ā„Ē„ė¤Ļ”¢„Ė„唼„ķ„ó¤Ī½ŠĪ¤ņ¼Q¤¹¤ė»ž¤Ė”¢¤Ž¤ŗ”¢„·„Ź„ׄ¹ńT¹ē¤ĪÄ_¤ß¤ņɽ¤¹„Ł„Æ„Č„ė{ wi }¤Č”¢ĘžĪæ®Ņ¤¬É½¤¹„Ł„Æ„Č„ė{ xi }¤ĪĘāĄŃĆĶ¤ņµį¤į¤ė”ŹR1”Ė”£ ĘāĄŃĆĶ¤Ļ”¢„Ł„Æ„Č„ė{ wi }¤Č„Ł„Æ„Č„ė{ xi }¤Īøž¤¤¬Ę±¤ø¤Ē¤¢¤ė»ž¤ĖŗĒ½j¤Č¤Ź¤ė¤Ī¤Ē”¢Ī¾„Ł„Æ„Č„ė“Ö¤Ī”Öøž¤”פĪŽkĆפĪęÅŁ¤ņɽ¤¹¼ÜÅŁ¤Č¤Ź¤ė”£¤ā¤·”¢„Ł„Æ„Č„ė¤ĪŤµ¤¬³Ź²½¤µ¤ģ¤Ę¤¤¤ė¤Č¤¹¤ė¤Č”¢ĘāĄŃĆĶ¤Ļ”¢„Ł„Æ„Č„ė¤Ī½ŖÅĄ“Ö¤Ī”ÖÕ{ß`”פĒ¤ā¤¢¤ė”£
É®Ēv¤Ļ”¢æĶ¹©„Ė„唼„ķ„󤬔¢Ęó¤Ä¤Ī¾šŹó”Ź³Ų{¤Ė¤č¤Ć¤ĘĶŌu¤·¤æ„Ł„Æ„Č„ė¤ČĘžĪ„Ł„Æ„Č„ė”Ė¤Ī”Ö“°ęŽkĆהפĒ¤Ļ¤Ź¤Æ”¢Ī¾„Ł„Æ„Č„ė¤Ī”Öøž¤¤ĪŽkĆפĪęÅŁ”פä”ÖÕ{ß`¤ĪZ¤µ”פņƤ¤¤ĘbĶż±éQ¤ņ¹Ō¤Ć¤Ę¤¤¤ė¤³¤ČO¤¬”¢”Ö³ĪĪØÅŖbĶż”פĪÄ_Ķץ¤ņ¼ēÄ„¤¹¤ė¤ā¤Ī¤Ą¤Č»×¤¦”£ ”Öøž¤¤ĪŽkĆפĪęÅŁ”פä”ÖÕ{ß`¤ĪZ¤µ”פĻ”¢ÉŌ³ĪÄź¤µ¤ņįĶʤ¹¤ėĪ©¾ģ¤Ą¤«¤é¤Ą”£ øķŗ¹¤ņįĶʤ·¤ĘæŹ¤į¤ėbĶż¤Ļ”¢Ł¤Ė”Ö³ĪĪØÅŖbĶż”פĒ¤¢¤ė”£
¤½¤³¤Ē”¢°Ź²¼¤Ė”¢”ÖæĶ¹©„Ė„唼„ķ„ó¤ĪĘ°ŗī¤¬”¢³ĪĪØÅŖbĶż¤Īśt³«¤Ē¤¢¤ė”פČø«Šö¤¹Ķż½y¤ņ”¢vĻ©¤¬Ć¤¤¤ėĮĒ»Ņ¤äæ®Ņ¤ĪčÅĄ¤«¤é¤Č”¢vĻ©¤¬½čĶż¤¹¤ė¾šŹó¤Ī C¤«¤é¤Ž¤Č¤į¤Ę¤ß¤æ”£
ĮĒ»Ņ¤äæ®Ņ¤ĪčÅĄ¤«¤éø«¤ė”Ö³ĪĪØÅŖ½čĶż”×
æĶ¹©„Ė„唼„ķ„󤬄ā„Ē„ė²½¤·¤č¤¦¤Č¤¹¤ėæĄ·ŠŗŁĖ¦¤ĪČÆĘ°ŗī¤¬”¢¤½¤ā¤½¤ā³ĪĪØÅŖ¤Ą¤Ć¤æ¤³¤Č¤ņ»×¤¤½Š¤·¤Ę¤¤¤æ¤Ą¤¤æ¤¤”£ ¼ĀŗŻ¤ĪæĄ·ŠŗŁĖ¦¤Ė¤Ŗ¤±¤ė”ÖČÆø½ž”פĻ”¢”ÖæĄ·ŠŗŁĖ¦Ėģ¤ĪƦŹ¬¶Ė¤Ė¤ĘÖø¤¹¤ėĖģÅÅ°Ģ¤¬č|ĆĶ°ŹÖ¤Č¤Ź¤Ć¤æ»ž¤Ė¤ė”ŹæŽ2”Ė”פȤµ¤ģ¤Ę¤¤¤æ¤¬”¢¤½¤Īč|ĆĶÅÅ°Ģ¤Ļ”¢WÄź¤·¤æÉwÄźÅÅ°Ģ¤Ē¤Ļ¤Ź¤«¤Ć¤æ”ŹR2”Ė”£
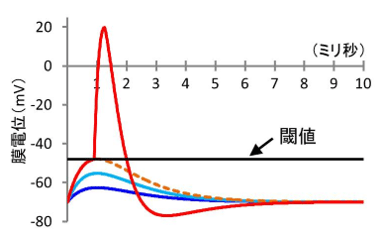
æŽ2””æĄ·ŠŗŁĖ¦¤ĪŗŁĖ¦Ėģ¤ĪĘ°ÅÅ°Ģ”ŹAction Potential”Ė¤Čč|ĆĶ¤Ī“Ų·ø””ŗŁĖ¦Ęā¤ĖĪ®Ęž¤·¤æ„¤„Ŗ„ó¤Ė¤č¤ėĖģÅÅ°Ģ¤ĪŹ¬¶Ė¤¬”Öč|ĆĶ”פņ±Ū¤Ø¤ė¤Č”¢”ÖƦŹ¬¶Ė”פȤ¤¤¦„Ż„ø„Ę„£„Ö„Õ„£”¼„É„Š„Ć„Æø½ž¤¬¤³¤ź”¢„Ń„ė„¹ÓX¤ĪĘ°ÅÅ°Ģ”Ź·”Ė¤¬ČÆŚ¤¹¤ė”פȤ¹¤ė”£””½ŠÖZ”§WebÖ¤ĪĖN²Ź³ŲŻÖZ”Ź2012ćQ4·ī3ĘüČĒ”Ė
”ÖŗŁĖ¦Ėģ¤ĪĪ¾ C¤ĪÅÅ°Ģŗ¹”ŹĖģÅÅ°Ģ”Ė¤¬č|ĆĶ¤ņ®¤Ø¤ė¤Č”¢„Ż„ø„Ę„£„Ö„Õ„£”¼„É„Š„Ć„Æ”ŹŁµ¢ ²”Ė¤¬¤«¤«¤ź”¢½ŠĪÅÅ°Ģ¤¬¾÷¤ĖÖø¤¹¤ė”פȤ¤¤¦æĄ·ŠŗŁĖ¦¤ĪČÆĘ°ŗī¤Ļ”¢Č¾Ę³„Č„é„ó„ø„¹„æ¤ņ»Č¤Ć¤æŗ¹Ę°vĻ©¤ĪĘ°ŗī¤Čō¤ė”£ ŗ¹Ę°vĻ©¤ĪĘ°ŗī¤¬č|ĆĶZÕf¤Ē¤Ļ³ĪĪØÅŖ¤Ė¤Ź¤ė°ŹÖ”¢æĄ·ŠŗŁĖ¦¤ĪČƤ¹¤ė”椷¤Ź¤¤¤ĪČ½Äź¤āč|ĆĶZÕf¤Ē¤Ļ³ĪĪØÅŖ¤Č¤Ź¤ė¤Ī¤ĻÉŌ»×µÄ¤Ē¤Ļ¤Ź¤¤”Ź»²¹Ķ«@ĪĮ5”Ė”£
¤·¤«¤ā”¢æĄ·ŠŗŁĖ¦¤ĪĘžĪæ®Ņ¤Īæ®Ņæ¶Éż¤Ļ100mVęÅŁ¤·¤«¤Ź¤¤”£¤¢¤ėĮTĢ£¤Ē¤Ļ”¢æĄ·ŠŗŁĖ¦¤Ų¤ĪĘžĪæ®Ņ¤Ļ”¢¾ļ¤Ėč|ĆĶZÕf¤ĖÉŗ¤Ć¤Ę¤¤¤ė¤Č¤āøĄ¤Ø¤ė”£ ¼ĀŗŻ¤ĪæĄ·ŠŗŁĖ¦¤Ē¤Ļ”¢»žĄŽ”¢„é„ó„Ą„ą¤ŹČÆø½ž”ŹOśČÆ”Ė¤¬ø«¤é¤ģ¤ė¤¬”¢¤½¤ģ¤Ļ”¢Č¾Ę³Ąß¼¤ņ·ŠŁx¤·¤ææĶ“Ö¤Ē¤¢¤ģ¤Š”¢”ÖĘžĪ„ģ„Ł„ė¤ņč|ĆĶ¤Ī„°„ģ”¼„¾”¼„óĘā¤ĖĄßÄź¤·¤Ę¤¤¤ė¤Ī¤Ą¤«¤é”¢øķĘ°ŗī¤ā¤¢¤ė¤Ą¤ķ¤¦”פČøĄ¤Ć¤Ę¤·¤Ž¤¤¤½¤¦¤Źø½ž¤Ē¤¢¤ė”Ź»²¹Ķ«@ĪĮ6”Ė”£
„Ž„«„ķ„Ć„Æ&„Ō„ƄĤĪæĶ¹©„Ė„唼„ķ„ó¤ā”¢„Õ„©„󔦄Ī„¤„Ž„óž¤ĪƱ½ŠĪ„Ŗ”¼„Č„Ž„Č„ó¤ā”¢æĄ·ŠŗŁĖ¦¤ĪĘ°ŗī¤ņĮĒľ¤Ė¤½¤Ī¤Ž¤Ž„ā„Ē„ė²½¤·¤æ¤æ¤į”¢“šĖÜvĻ©„ā„Ē„ė¤ĪĘ°ŗī¤ņ³ĪĪØÅŖ¤Č¤·¤æ¤Č¤Ļ¹Ķ¤Ø¤é¤ģ¤ė”£ æĄ·ŠvĻ©¤ĪbĶżśt³«¤ņĮĒľ¤Ėč»”¤¹¤ė¤Č”¢¤½¤ģ¤Ļ”¢”Ö„Ī„¤„ŗČÆŚ¤ņČ¼¤¦³ĪĪØŌę”פČø«¤Ø¤ė¤Ī¤Ą¤ķ¤¦”£
æĄ·ŠŗŁĖ¦¤¬½čĶż¤¹¤ėĘžĪ¾šŹó”ŹĘžĪæ®Ņ·²”Ė¤Ī½j¤¤µ¤¬”Ö³ĪĪØÅŖ½čĶż”פņĶפ¹¤ė
æĄ·ŠŗŁĖ¦¤Ų¤Īæ®ŅĘžĪ¤ĪĖÜæō¤Ļ¾ļ¤ĖóH¤Æ“°ęŽkĆפ·¤Å¤é¤¤¤æ¤į”¢”Ö¤Ū¤ÜŽkĆפ·¤æÓXŻ”פņƤ¤¤ĘbĶż¤ņæŹ¤į¤ėµ¤¬ć~ƤĄ¤Ć¤æ¤Č¤¤¤Ø¤ė¤Ī¤Ē¤Ļ¤Ź¤¤¤Ą¤ķ¤¦¤«”©
¤½¤ā¤½¤ā”¢æĶ¹©„Ė„唼„ķ„ó¤ā”¢ø½¼Ā¤ĪæĄ·ŠŗŁĖ¦¤ā”¢ŽkČĢ¤Ė”¢„·„Ź„ׄ¹ńT¹ē¤ĪøÄæō¤Ļ¾ļ¤ĖóH¤¤”£ óH¤¤¾ģ¹ē¤Ė¤Ļ”¢1000¤ņĶ„¤Ė®¤Ø¤ė„·„Ź„ׄ¹¤¬ńT¹ē¤Ė¤č¤Ć¤Ę”¢iĆŹ„Ė„唼„ķ„󤫤é¤Īæ®Ņ¤ņp¤±¤Ę¤¤¤ė”£ ¤Ä¤Ž¤ź”¢ĘžĪ¾šŹó¤ņĢĻ¼°²½¤¹¤ė„Ł„Æ„Č„ė{ xi }¤Č³Ų{¤Ė¤č¤źĶŌu¤·¤æĶŌu¤·¤æ¾šŹó¤ņĢĻ¼°²½¤¹¤ė„Ł„Æ„Č„ė{ wi }¤Ī¼”øµæō¤Ļ¶¦¤Ė¾ļ¤Ė½j¤¤¤”£ ņ¤Ć¤Ę”¢Ī¾„Ł„Æ„Č„ė¤¬ę¤Æʱ¤øµøž¤ņøž¤Æ²Ä¦Ą¤Ļ¾ļ¤ĖÄ椤¤Č¤¤¤Ø¤ė”£ Źø¾Ļ”¢²»³Ś”¢³Ø²č”¢É÷·ŹÅł¤ĪæĶ“Ö¤¬“ž¤Č¤¹¤ė¾šŹó¤ā”¢ĘóÅŁ¤Čʱ¤øɽø½¤Ė½Š²ń¤¦¤³¤Č¤¬Ģµ¤¤¤Č»×¤Ø¤ėę¤ĖŹ£æō¤Ī¾šŹó¤¬ŽkĆפ¹¤ė³ĪĪؤĻÄ椤¤ā¤Ī¤Ą”£
½ćæ褏æō³ŲĄ¤Äc¤Ė¤Ę”¢ÅłŅ”Ź=”Ė¤¬ĮTĢ£¤¹¤ė”Öø·³Ź¤ŹŽkĆהפ¬Ä_ĶפĒ¤¢¤ź”¢æō³ŲĄ¤Äc¤Ē¤ĪÅłŅ”Ź=”Ė¤ĪÄ_Ķץ¤ĻÅöĤȤ·¤Ę¤ā”¢¤·¤«¤·”¢æĶ“Ö¤ĪĖN¤¬¹Ō¤¦„Ē”¼„æ½čĶż¤Ė¤Ŗ¤¤¤Ę¤Ļ”¢ÅłŅ”Ź=”Ė¤¬Ą®Ī©¤¹¤ė¤³¤Č¤Ļ¤Ū¤Č¤ó¤É¤Ź¤¤¤Ī¤Ē¤¢¤ė”£ ¤½¤ĪĮTĢ£¤Ē”¢Źø¾Ļ”¢²»³Ś”¢³Ø²č”¢É÷·Ź”¢Åł¤Ī¾šŹó½čĶż¤Ė¤Ŗ¤¤¤Ę¤Ļ”¢ÅłŅ”Ź=”Ė¤ĪÄ_Ķ×ÅŁ¤ĻÄ椤¤Č¤ā¤¤¤Ø¤ė”£ ø½¼ĀĄ¤Äc¤Ī¾šŹó¤Ļ”¢“ž¤āč»”ÅĄ¤āŹŃ²½¤·¤Ę¤¤¤ė¤Ī¤¬ÄĢ¾ļ¤Ē¤¢¤ź”¢¤Ė”¢æ®Ņ¤Ė¤Ļ„Ī„¤„ŗ¤ā“Ž¤Ž¤ģ¤ė”£ ø½¼ĀÅŖ¤Ė¤Ļ”¢Zō”Ź¢ā”Ė¤Ė¤Ę”¢ÓXŻ¤ņČ½ŹĢ¤·¤Ę”¢bĶż¤ņśt³«¤¹¤ė¤·¤«¤Ź¤¤¤Č¤āøĄ¤Ø¤ė”£
¤Č¤¤¤¦¤³¤Č¤Ļ”¢ÅłŅ”Ź=”ĖĘ°ŗī¤ņĆę擤ĖĮȤßĪ©¤Ę¤é¤ģ¤æø½ŗߤĪ„ķ„ø„Ć„Æ½øĄŃvĻ©¤Ļ”¢Zō”Ź¢ā”Ė¤¬Ćęæ“¤Č¤Ź¤ėŹø¾Ļ”¢²»³Ś”¢³Ø²č”¢É÷·Ź”¢Åł¤Ī¹āÅŁ¤Ź¾šŹó½čĶż¤Ė¤Ļøž¤¤¤Ę¤¤¤Ź¤¤¤Č¤¤¤¦¤³¤Č¤Ė¤Ź¤é¤Ź¤¤¤«”©
„ķ„ø„Ć„Æ½øĄŃvĻ©¤Ļ”¢ŽkČĢ¤Ė”¢æŽ3¤Ī¤č¤¦¤ŹææĶżĆĶɽ¤ĪĘ°ŗī¤ņƤ¤¤ĘĄß¼¤µ¤ģ¤ė”£””Čę³ÓÅŖĘžĪĖÜæō¤Ī¾Æ¤Ź¤¤AND¤äNOR¤Ź¤É¤Ī“šĖÜvĻ©¤Ē¤¢¤ė”£“šĖÜvĻ©¤Ļ”¢ææĶżĆĶɽ¤ĪĘžĪ”ŹX1”Ė¤ČĘžĪ”ŹX2”Ė¤ĪĮČ¤ß¹ē¤ļ¤»¤¬“°ęŽkĆ×”Ź=”Ė¤·¤æ¹Ō¤Ī”Ö½ŠĪ”ŹY”Ė¤ĪĶó¤ĪĆĶ”פņ½ŠĪ¤¹¤ė”£
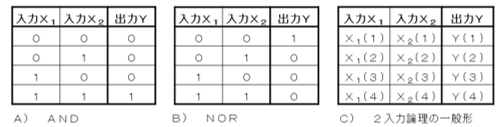
æŽ3””„³„ó„Ō„唼„æ¤Ē»Č¤ļ¤ģ¤ė“šĖܱéQvĻ©¤ĪææĶżĆĶɽ¤ĪĪć””2ĘžĪ¤ĪææĶżĆĶɽ¤ĪŽkČĢ·Į¤Ļ”ŹC”Ė¤Ī¤č¤¦¤Ė¤Ź¤ė¤¬”¢³ĪĪØÅŖbĶż¤Ī¾ģ¹ē¤Ļ”¢·QæōĆĶ¤¬³ĪĪØĆĶ¤Č¤Ź¤ź¤¦¤ė”£””½ŠÖZ”§É®ĒvŗīĄ®
Žkµ”¢ø½¼ĀĄ¤Äc¤ĪóH¼”øµ¾šŹó¤Ī½čĶż¤ĖŗĒŬ²½¤µ¤ģ¤ææĶ¹©„Ė„唼„ķ„󔏷²”Ė¤ĪææĶżĆĶɽ¤Ļ”¢æŽ4¤Ī¤č¤¦¤Ź¾ļ¤ĖĘžĪĖÜæō¤Ī½j¤¤ŹÉ½¤Č¤Ź¤ė¤Ą¤ķ¤¦”£ ¤Ė”¢·Q¹Ō¤Ī½ŠĪ¤ĪĶó¤ĪĆĶ¤ņ”¢”Ö0”Į1¤Ī“Ö¤ĪĆĶ¤ņĘD¤ė³ĪĪØĆĶ”פȤ·¤Ę”¢”ÖĆĶ1¤¬½ŠĪ¤µ¤ģ¤ė³ĪĪؔפņ椹¤Ī¤¬¼ĀĆÖć~ƤȤŹ¤ė”£
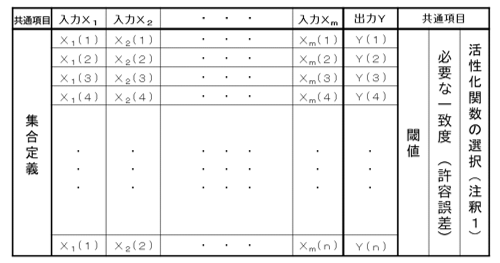
æŽ4””„Ė„唼„ķ„ó„ā„Ē„ė¤ņɽø½¤¹¤ėææĶżĆĶɽ¤ĪĪć””¾ļ¤ĖóHĘžĪ¤Ē¤¢¤ź”¢ĘžĪ¤ä½ŠĪ¤ĪĶó¤ĪĆĶ¤Ė”Ö³ĪĪØĆĶ”פ¬ÅŠ¾ģ¤¹¤ė¤č¤¦¤ŹĖÜɽ¤Ī¤č¤¦¤ŹÉ½¤Č¤Ź¤ė”£ ³ĪĪØÅŖbĶż¤Ė¤Ļ”¢ĒŲ·Ź¤Č¤·¤Ę”¢”Ö²æ¤Ī½ø¹ē¤Ė¤Ę³ĪĪؤņĢ䬤Ė¤¹¤ė¤«”פ䔢”Ö„µ„ó„ׄėæō”Ź¹ē¼”Ė”פņ«³Ī¤Ė¤·”¢¤Ė”¢”ÖZō”Ź¢ā”Ė¤¬Ą®¤źĪ©¤Ä¤Čø«Šö¤¹»ž¤Ī”ŲĶפŹŽkĆ×ÅŁ”Ł”¢¤ā¤·¤Æ¤Ļ”¢”ŲįĶĘøķŗ¹”Ł”¢Åł¤ņ«³Ī²½¤¹¤ėĶפ¬¤¢¤ė¤æ¤į”¢¤½¤Ī¤č¤¦¤Ź¹ąÖ`¤ņµŗܤ¹¤ėĶó¤ņ¼{²Ć¤·¤Ę¤¤¤ė”£¤Ź¤Ŗ”¢¤³¤Īɽ¤Ļ”¢1øĤĪ„Ė„唼„ķ„ó¤ĪĘž½ŠĪbĶż¤ņÄź±I¤·¤¦¤ė¤Ą¤±¤Ē¤Ļ¤Ź¤Æ”¢Īąō¤Īµž¤Ī¾šŹó¤ņ½čĶż¤¹¤ėŹ£æōøÄ”ŹnøĤĪ”Ė„Ė„唼„ķ„ó½ø¹ēę¤ĪĘž½ŠĪbĶż¤ņÄź±I¤¹¤ėææĶżĆĶɽ¤Č¤¹¤ė¤³¤Č¤ā¤Ē¤¤ė”£””½ŠÖZ”§É®ĒvŗīĄ®
¤½¤Ī¤č¤¦¤ŹæŽ4¤ĪææĶżĆĶɽ¤ņ”¢æŽ3¤ĪææĶżĆĶɽ¤ņ·e¤Ä“šĖÜvĻ©¤ņ½jĪĢ¤ĖĮČ¤ß¹ē¤ļ¤»¤Ęɽø½¤·Ä¾¤¹¤³¤Č¤Ļ²Ä¦¤Ą¤ķ¤¦”£ ø½¤Ė”¢ø½ŗßÄ󶔤µ¤ģ¤Ę¤¤¤ėAI„µ”¼„Ó„¹¤ņÄ󶔤·¤Ę¤¤¤ė„µ”¼„Š¤Ī½øĄŃvĻ©¤Ļ”¢2ĘžĪ¤Ē¤ĻĢµ¤¤¤«¤ā¤·¤ģ¤Ź¤¤¤¬”¢Čę³ÓÅŖ¾Ææō¤ĪĘžĪ¤ĪNAND¤äNOR¤ņ½jĪĢ¤ĖĮČ¤ß¹ē¤ļ¤»¤ævĻ©¤«¤é¹½Ą®¤µ¤ģ¤Ę¤¤¤ė”£
¤·¤«¤·”¢¾Æ¤Ź¤Æ¤Č¤ā”¢„Õ„©„󔦄Ī„¤„Ž„ó¤ä”¢„Ž„«„ķ„Ć„Æ&„Ō„ƄĤĪŗ¢¤Ļ”¢”ÖæĶ¹©Ę¬ĖN³«ČƤĖ¤Ļ”¢æŽ4¤Ī¤č¤¦¤Ź¾ļ¤ĖĘžĪĖÜæō¤ĪóH¤¤³ĪĪØÅŖbĶż¤ņƤ¤¤ė¤Ī¤¬ĮĒľ¤Ą”×¤Č¹Ķ¤Ø¤é¤ģ¤Ę¤¤¤æ”£
¤Č¤¤¤¦¤³¤Č¤Ļ”¢„Ė„唼„ķ„󤬹Ō¤¦±éQ¤ņĢĻ¤·¤ææŽ4¤ĪææĶżĆĶɽ¤ĪĘ°ŗī¤ņ¹Ō¤¦“šĖÜbĶżvĻ©¤ņƤ¤¤æµ¤¬”¢AIvĻ©¤ĪĄß¼¤Ėøž¤Æ¤Ī¤Ē¤Ļ¤Ź¤¤¤«”©óHĘžĪ¤Ī³ĪĪØÅŖbĶż¤ņƤ¤¤ė¤Č”¢ĖN¤Ī¤č¤¦¤Ė”¢¼SÅŖ¤Ė¾Æ¤Ź¤¤¾ĆäJÅÅĪ¤ĒōÅŖ¾šŹó½čĶż¤ņ¹Ō¤Ø¤ė¤Č¤¤¤¦¤³¤Č¤Ź¤Ī¤Ą¤ķ¤¦¤«”©
ø½Āå¤Ī½øĄŃvĻ©¤Ļ”¢CMOS¶\½Ń¤ņƤ¤¤Ę”¢Čę³ÓÅŖĘžĪĖÜæō¤Ī¾Æ¤Ź¤¤AND¤äNOR¤Ź¤É¤ņ“šĖÜvĻ©¤Č¤·”¢vĻ©ĢĻ¤ņĄŃ¤ßÖ¤²¤ė¾}Ė”¤ņÅöĤȤ·¤ĘĶč¤æ¤¬”¢ŗ£ŽkÅŁ”¢¾ļ¤ĖóHĘžĪ¤Ī³ĪĪØÅŖbĶż¤Īć~ĆĄ¤ņ¹Ķ¤Ø¤Ę¤ß¤ė¤Ł¤¤Ē¤Ļ¤Ź¤Ī¤Ē¤Ļ¤Ź¤¤¤Ą¤ķ¤¦¤«¤Č»×¤Ø¤ėńT²Ģ¤Č¤Ź¤Ć¤æ”£
R
1. „Ž„«„ķ„Ć„Æ&„Ō„ƄĤĪ„ā„Ē„ė¤Ē¤Ļ”¢æĶ¹©„Ė„唼„ķ„ó¤Ī±éQĘ°ŗī¤ņ”¢„·„Ź„ׄ¹ńT¹ē¤ĪÄ_¤ß¤ņɽ¤¹„Ł„Æ„Č„ėĪĢ { wi; i=1,2,3,”¦”¦”¦N }¤Č”¢ĘžĪæ®Ņ¤¬É½¤¹„Ł„Æ„Č„ėĪĢ { xi; i=1,2,3,”¦”¦”¦N }¤ĪĘāĄŃĆĶ¤ņĄč¤ŗµį¤į”¢¤½¤ĪĘāĄŃĆĶ¤Čč|ĆĶ”Źb”Ė¤Īŗ¹¤Ė”¢Ą²½“Ųæō (¦Õ) ¤ņŗīƤµ¤»¤Ę½ŠĪĆĶ¤ņµį¤į¤ė”Ź»²¹Ķ«@ĪĮ 2”Ė”£
y=¦Õ() -b
ø½ŗߤĒ¤Ļ”¢“Ųæō (¦Õ) ¤Č¤·¤Ę”¢²¼æŽ¤Ī¤č¤¦¤ĖĶĶ”¹¤Ź“Ųæō„愤„פ¬»ī¤µ¤ģ¤Ę¤Ŗ¤ź”¢Ćż¤Ė±ž¤ø¤ĘĀŁI¤µ¤ģ¤ė”£
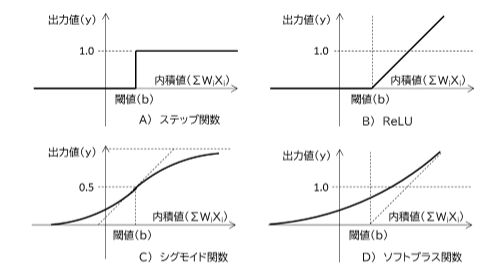
2. ¤½¤Īč|ĆĶ”Źč|ĖģÅÅ°Ģ”Ė¤Ļ”¢”ÖŗŁĖ¦Ėģ¤ĖŁTŗߤ¹¤ė„Į„ć„Ķ„ė·ź¤«¤éĪ®Ęž¤¹¤ė„Ź„Č„ź„¦„ą„¤„Ŗ„ó”Ź+”ĖĪĢ¤Č”¢Ī®½Š¤¹¤ė„«„ė„·„¦„ą„¤„Ŗ„ó”Ź+”ĖĪĢ”¢Ī®Ęž¤¹¤ėŁeĮĒ„¤„Ŗ„ó”Ź-”ĖĪĢ¤¬Äą¤ź¹ē¤¦ÅÅ°Ģ”פȤµ¤ģ¤ė¤ā¤Ī¤Ī”¢ø·Ģ©¤Ė¤Ļ”¢”Ö¤½¤ģ¤é¤Ī„¤„Ŗ„ó¤ĪĪ®ĘžĪĢ¤Ė¤č¤Ć¤Ę”£ÅÅ°Ģ¤Ī¾Öøø½ž¤¬¤³¤ė³ĪĪؤ¬ŹŃ¤ļ¤ė”פæ¤į”¢Ę°ŗī¤¬„°„ģ”¼¤ŹÕJ°Ļ¤¬¤¢¤ė¤Č¤µ¤ģ¤Ę¤¤¤ė”Ź»²¹Ķ«@ĪĮ5”Ė”£
»²¹Ķ«@ĪĮ
1. Nilsson, N. J., "Probabilistic Logic" Artificial Intelligence, vol.28, pp. 71-87, 1986
2. Neumann, J. V., "Probabilistic logics and the synthesis of reliable organisms from unreliable components", Automata Studies (ed. by C. E. Shannon and J. McCarthy), Princeton University Press, Princeton, N.J., 1956.
3. McCulloch W. S. & Pitts, W., "A logical calculus of the ideas immanent on nervous activity." Bulletin of mathematical biophysics, vol. 5, pp. 115–133, 1943.
4. McCulloch W. S.; "What is a Number, That a Man May Know it, And a Man, That He May Know a Number?" General Semantics Bulletin, vol. 26/27, pp.7–18, 1960.
5. WebÖ¤ĪĖN²Ź³ŲŻÖZ (2012ćQ4·ī3ĘüČĒ)¤Ī”Öč|ĆĶ”פĪ¹ą
6. »ūi½ēĒ·å\”¢”ÖĖN¤Čō¦¤ĪńĶż³Ų”×”¢ńĄø¦|”¦ÅÅ»ŅČĒ””Vol.8, No.1, 2020ćQ2·īŅ


